area voluta e creata al solo scopo informativo
scolastico
INTERNET FREE
ZAPPING
Il quesito
Data una circonferenza di raggio unitario e centro O,
tracciare una semiretta S uscente da O e intersecante la circonferenza in
un punto Q. Indicato con P un generico punto di S esterno alla
circonferenza, tracciare da esso le due tangenti alla circonferenza: siano
A e B i punti di tangenza. Indicata con x la lunghezza del segmento PQ,
trovare il limite per x tendente ad infinito del rapporto: k =(AQ+QB):AB.
Come si fa a trovare i tre segmenti AQ , QB e AB?
La risposta
Per prima cosa osserviamo che per rispondere alla domanda posta dal problema (calcolo del limite) si può procedere mediante considerazioni di natura geometrica. Di seguito è riportata la geometria del problema al variare dell’incognita x:
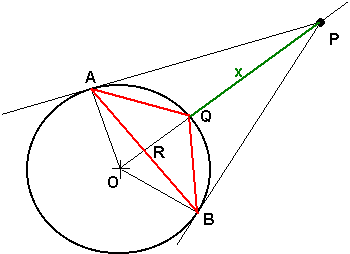
L’ultima figura è quella relativa al caso 
. Dall’esame
di tale figura si deduce che in tali condizioni si ha:
AB = 2
AQ = BQ = 
E quindi:
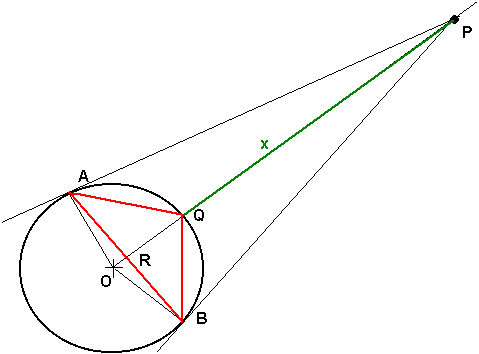
Volendo comunque ricavare le espressioni dei tre segmenti AB, AQ e QB in funzione di x si può procedere come segue. Si consideri la figura qui sotto, in cui è riportata una generica posizione del punto P:
In base ai dati del problema si ha:
AO = BO = OQ = 1
OP = 1 + x
In genere in questo tipo di problemi è conveniente utilizzare i triangoli rettangoli, in quanto il Teorema di Pitagora consente di esprimere un lato in funzione degli altri.
Innanzi tutto osserviamo che la semiretta è un asse di simmetria della figura e quindi, ad esempio, AQ = BQ. Per prima cosa calcoliamo il segmento AP, che è un cateto del triangolo rettangolo OAP (il triangolo è rettangolo perché la tangente alla circonferenza è sempre ortogonale al raggio):
Adesso è possibile calcolare il segmento AR che è l’altezza relativa all’ipotenusa del triangolo rettangolo OAP, la cui area è data da:
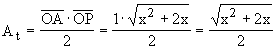
L’altezza relativa all’ipotenusa si ottiene dividendo la doppia area del triangolo per l’ipotenusa:
Se ora applichiamo il Teorema di Pitagora al triangolo OAR, che è rettangolo per motivi di simmetria, si ottiene (si omettono i passaggi):
da cui:
Infine, applicando il teorema di Pitagora al triangolo ARQ si ha:
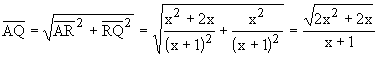
In conclusione si ha:
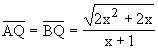
Pertanto:
