area voluta e creata al solo scopo informativo scolastico
          INTERNET FREE ZAPPING      

1. Cerchiamo di capire innanzi tutto cosa vuol dire calcolare un limite di una funzione.

   Quando si calcola il limite:

   

   si intende studiare il comportamento della funzione quando x è "vicino a x₀"; questa precisazione è importante in quanto bisogna avere ben presente che il calcolo del limite si disinteressa completamente di quello che accade alla funzione f(x) quando x = x₀. Questo concetto è molto difficile da comprendere, ma forse un esempio può essere d'aiuto. Consideriamo la funzione:

   

    

   Se provi a disegnare questa funzione dovresti avere una retta con un "buco" in x = 2.

   Ora ci domandiamo qual è il limite di f(x) per x che tende a 1. La risposta dovrebbe essere abbastanza semplice. il limite è 3.

   Ma quanto vale il limite di f(x) per x che tende a 2?

   Se hai intenzione di rispondere vale 0 (anch'io ho risposto così la prima volta che ho visto questo esempio!) soffermati un momento su quello che abbiamo detto prima.

   Il limite della funzione non dipende da quanto vale la funzione in x₀ ma da come si comporta la funzione nei punti vicini a x₀.

   Poiché nel nostro esempio la funzione, per punti vicini a x₀, vale x + 2 allora il limite per x che tende a x₀ è 4.

2. Il calcolo dei limiti si basa sui seguenti risultati dell'analisi Matematica:

   1. i teoremi sulle operazioni sui limiti (ad esempio: il limite di una somma è pari alla somma dei limiti, ecc.), che qui non vengono elencati in quanto si trovano su tutti i libri di testo;

   2. il teorema sulle funzioni continue, che dice che se una funzione è continua allora il limite si ottiene semplicemente sostituendo il valore di x₀ al posto della x.

   Se ora consideri nuovamente l'esempio iniziale, ti accorgerai sicuramente che il teorema sulle funzioni continue non può applicarsi quando x₀ = 2. Questo accade perchè la funzione data non è continua in x₀!

   Come esempio calcoliamo il limite:

   

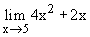
   Si tratta di una funzione continua e quindi il limite si ottiene semplicemente sostituendo 5 al posto della x ottenendo 110.

   Le cose non sono sempre così facili. Spesso, sostituendo x₀ al posto della x si ottiene una forma indeterminata (detta anche forma di indecisione) nel senso che non è possibile dire quanto è il limite. Sul tuo libro di testo troverai senz'altro l'elenco completo delle forme indeterminate. Quando ci si trova davanti a una forma indeterminata ciò non vuol dire che il limite non esiste, ma semplicemente che la semplice sostituzione di x₀ a x non è sufficiente a risolvere il calcolo.

   Supponiamo di voler calcolare il limite:

   

   Se sostituiamo al posto della x il valore 1 otteniamo la forma indeterminata 0/0. Infatti sia il numeratore che il denominatore tendono a zero e applicando il teorema sul limite di un rapporto si ottiene appunto 0/0. Dunque questo metodo di risoluzione non ci aiuta.

   Cosa succede se al posto della x mettiamo 1,1? Io l'ho calcolato con la calcolatrice e ho ottenuto: 2,1.

   Ripetiamo la stessa operazione con x = 1,01. Si ottiene 2,01.

   Con x = 1,001 si ottiene 2,001.

   Si noterà che x sta tendendo a 1 mentre f(x) sembra tendere a 2. Ciò accade per punti via via più vicini a x = 1. Ricordando che il calcolo del limite si disinteressa di cosa accade proprio in x₀ (in questo caso x₀ = 1) ma tiene conto di quello che accade in punti vicini iniziamo a sospettare che il limite dell'esempio sia pari a 2. Per dimostrarlo dobbiamo risolvere la forma indeterminata.

   Una forma indeterminata può essere risolta in tre modi:

   1. eseguendo delle trasformazioni della funzione data in modo da semplificarla;

   2. sfruttando il Teorema del confronto e la conoscenza dei limiti calcolati in precedenza;

   3. utilizzando il Teorema di De L'Hopital

   Con riferimento al primo metodo la funzione considerata nell'esempio si può scrivere (ricordando il prodotto notevole differenza di due quadrati):

   

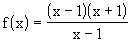
   Sritta la funzione in questo modo, si vede che è possibile operare una semplificazione ottenendo:

   f(x) = x + 1

   da cui è ora evidente che il limite risulta pari a 2.

   Con quanto detto non si pretende di fornire una risposta esauriente circa il calcolo dei limiti, ma solo una prima introduzione. Tuttavia i concetti esposti sono quelli fondamentali.