area voluta e creata al solo scopo informativo scolastico
          INTERNET FREE ZAPPING      

La ricerca di una funzione che soddisfa le condizioni date è abbastanza complicata, pertanto tentiamo di risolvere il problema per passi.

1. Cerchiamo una funzione che tende a un limite finito quando x tende a infinito

Sappiamo che alcune funzioni algebriche fratte soddisfano questa condizione: esse sono quelle in cui numeratore e denominatore sono due polinomi dello stesso grado. Ad esempio:

è una funzione che soddisfa la condizione 1).

Essa tuttavia non può risolvere il nostro problema in quanto:

1. il limite a cui tende per x che tende a 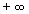, cioè 1, è uguale al limite per x che tende a ;

2. la funzione non è continua, presentando un punto di discontinuità in x = -1

Proviamo ad eliminare l'inconveniente b)

La funzione non è continua in x = -1 perché in corrispondenza di tale punto si annulla il denominatore. Dunque ci serve un denominatore che non si annulla per nessun valore di x. La prima cosa che viene in mente è prendere un denominatore del tipo:

A questo punto l'inconveniente b) è rimosso e ricordando che per avere un limite finito numeratore e denominatore devono essere dello stesso grado la funzione:

soddisfa ancora la condizione 1).

Resta da rimuovere l'inconveniente a), infatti la funzione tende a 1 in entrambi i casi. Prima di procedere oltre facciamo il seguente ragionamento.

Supponiamo di riuscire a trovare una funzione continua tale che il limite per x che tende sia uguale ma di segno opposto a quello per x che tende a .

Sia L il valore assoluto di tale limite e sia g(x) il nome di tale funzione. Consideriamo ora la funzione ottenuta aggiungendo a g(x) la costante K:

f(x) = K + g(x)

Per il teorema sul limite di una somma di funzioni si ha che f(x) tende a :

K + L

per x che tende a

K - L

per x che tende a

Se ora imponiamo le condizioni assegnate si ha il sistema lineare di due equazioni in due incognite:

che risolto fornisce:

K = 5/2

L = 1/2

In base a quanto detto quello che resta da fare è cercare la funzione g(x). La difficoltà sta nel fatto che le funzioni algebriche in cui numeratore e denominatore sono dello stesso grado (caso in cui il limite è finito) sono tali che hanno lo stesso limite (con lo stesso segno) sia per x che tende a sia per x che tende a . Inoltre ci serve un denominatore che non si annulla mai.

Consideriamo allora l'espressione:

che per x molto grande è equivalente a | x | (modulo di x). Questa caratteristica è per noi fondamentale in quanto ci consente di scrivere la funzione:

che è tale che:

Per ottenere la funzione g(x) è sufficiente allora moltiplicare la precedente per 1/2, ottenendo:

In conclusione la funzione cercata è (altre funzioni sono possibili, prova a cercarne un'altra seguendo lo stesso ragionamento):

Commento. Il quesito proposto presenta come detto una risoluzione tutt'altro che semplice. Il consiglio che posso darti è cercare di ragionare in modo da capire cosa cercare. Ti faccio notare che dovendo risolvere questo esercizio la cosa importante era riuscire a capire che tutto si riduceva a trovare una funzione il cui limite cambiasse segno passando da a .